Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
Image 2
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 3
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
Image 4
Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
$Image 5 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 5
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 6
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 7

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 8

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 9
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 10
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 11

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 12

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 13

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 14
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 15

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)

Good articles

Image 1
Thoralf Skolem, after whom the paradox is named

In mathematical logic and philosophy, Skolem's paradox is the apparent contradiction that a countable model of first-order set theory could contain an uncountable set. The paradox arises from part of the Löwenheim–Skolem theorem; Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as non-absoluteness. Although it is not an actual antinomy like Russell's paradox, the result is typically called a paradox and was described as a "paradoxical state of affairs" by Skolem.

In model theory, a model corresponds to a specific interpretation of a formal language or theory. It consists of a domain (a set of objects) and an interpretation of the symbols and formulas in the language, such that the axioms of the theory are satisfied within this structure. The Löwenheim–Skolem theorem shows that any model of set theory in first-order logic, if it is consistent, has an equivalent model that is countable. This appears contradictory, because Georg Cantor proved that there exist sets which are not countable. Thus the seeming contradiction is that a model that is itself countable, and which therefore contains only countable sets, satisfies the first-order sentence that intuitively states "there are uncountable sets". (Full article...)
Image 2
A Doyle spiral of type (8,16) printed in 1911 in Popular Science as an illustration of phyllotaxis. One of its spiral arms is shaded.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.

Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or early 1990s. However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early 1900s. (Full article...)
Image 3
A three-page book embedding of the complete graph $K 5$ . Because it is not a planar graph, it is not possible to embed this graph without crossings on fewer pages, so its book thickness is three.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

Every graph with $n$ vertices has book thickness at most $\lceil n/2\rceil$ , and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, every planar graph has book thickness at most four. It is NP-hard to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. (Full article...)
Image 4
Klaus Friedrich Roth (29 October 1925 – 10 November 2015) was a German-born British mathematician who won the Fields Medal for proving Roth's theorem on the Diophantine approximation of algebraic numbers. He was also a winner of the De Morgan Medal and the Sylvester Medal, and a Fellow of the Royal Society.

Roth moved to England as a child in 1933 to escape the Nazis, and was educated at the University of Cambridge and University College London, finishing his doctorate in 1950. He taught at University College London until 1966, when he took a chair at Imperial College London. He retired in 1988. (Full article...)
Image 5
Malfatti circles

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.

Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle.
A simple construction of the Malfatti circles was given by Steiner (1826), and many mathematicians have since studied the problem. Malfatti himself supplied a formula for the radii of the three circles, and they may also be used to define two triangle centers, the Ajima–Malfatti points of a triangle. (Full article...)
Image 6
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.

In technical terms, QED can be described as a very accurate way to calculate the probability of the position and movement of particles, even those massless such as photons, and the quantity depending on position (field) of those particles, and described light and matter beyond the wave-particle duality proposed by Albert Einstein in 1905. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. It is the most precise and stringently tested theory in physics. (Full article...)
Image 7
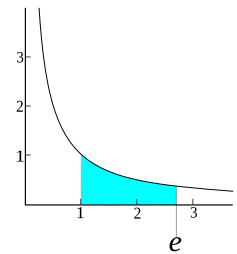
Graph of the equation $y = 1/ x$ . Here, $e$ is the unique number larger than 1 that makes the shaded area under the curve equal to 1.

The number $e$ is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted $\gamma$ . Alternatively, $e$ can be called Napier's constant after John Napier. The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest.

The number $e$ is of great importance in mathematics, alongside 0, 1, $π$ , and $i$ . All five appear in one formulation of Euler's identity $e^{i\pi }+1=0$ and play important and recurring roles across mathematics. Like the constant $π$ , $e$ is irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficients. To 30 decimal places, the value of $e$ is: (Full article...)
Image 8
A graph with three components

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.

The number of components in a given graph is an important graph invariant, and is closely related to invariants of matroids, topological spaces, and matrices. In random graphs, a frequently occurring phenomenon is the incidence of a giant component, one component that is significantly larger than the others; and of a percolation threshold, an edge probability above which a giant component exists and below which it does not. (Full article...)
Image 9

Official portrait, 2014

José Félix Mendieta Villarroel (born 15 November 1958) is a Bolivian politician and trade unionist who served as a member of the Chamber of Deputies from Cochabamba, representing circumscription 28 from 2010 to 2015.

Though educated in pedagogy, Mendieta spent most of his career in commercial driving, climbing the ranks of the sector's trade unions to eventually become general secretary of the Sacaba Mixed Motor Transport Union. Though traditionally conservative, under the leadership of figures like Mendieta, many of the country's drivers' unions were reoriented towards the left. (Full article...)
Image 10

Berlin, 1959

Andrew Mattei Gleason (1921–2008) was an American mathematician who made fundamental contributions to widely varied areas of mathematics, including the solution of Hilbert's fifth problem, and was a leader in reform and innovation in mathematics teaching at all levels. Gleason's theorem in quantum logic and the Greenwood–Gleason graph, an important example in Ramsey theory, are named for him.

As a young World War II naval officer, Gleason broke German and Japanese military codes. After the war he spent his entire academic career at Harvard University, from which he retired in 1992. His numerous academic and scholarly leadership posts included chairmanship of the Harvard Mathematics Department and the Harvard Society of Fellows, and presidency of the American Mathematical Society. He continued to advise the United States government on cryptographic security, and the Commonwealth of Massachusetts on mathematics education for children, almost until the end of his life. (Full article...)
Image 11
Hendrik Antoon Lorentz (right) after whom the Lorentz group is named and Albert Einstein whose special theory of relativity is the main source of application. Photo taken by Paul Ehrenfest 1921.

The Lorentz group is a Lie group of symmetries of the spacetime of special relativity. This group can be realized as a collection of matrices, linear transformations, or unitary operators on some Hilbert space; it has a variety of representations. This group is significant because special relativity together with quantum mechanics are the two physical theories that are most thoroughly established, and the conjunction of these two theories is the study of the infinite-dimensional unitary representations of the Lorentz group. These have both historical importance in mainstream physics, as well as connections to more speculative present-day theories. (Full article...)
Image 12
The small set expansion hypothesis or small set expansion conjecture in computational complexity theory is an unproven computational hardness assumption. Under the small set expansion hypothesis it is assumed to be computationally infeasible to distinguish between a certain class of expander graphs called "small set expanders" and other graphs that are very far from being small set expanders. This assumption implies the hardness of several other computational problems, and the optimality of certain known approximation algorithms.

The small set expansion hypothesis is related to the unique games conjecture, another unproven computational hardness assumption according to which accurately approximating the value of certain games is computationally infeasible. If the small set expansion hypothesis is true, then so is the unique games conjecture. (Full article...)

Did you know

... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
... that The Math Myth advocates for American high schools to stop requiring advanced algebra?

Did you know...

...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
...that it is possible for a three-dimensional figure to have a finite volume but infinite surface area, such as Gabriel's Horn?
... that as the dimension of a hypersphere tends to infinity, its "volume" (content) tends to 0?
...that the primality of a number can be determined using only a single division using Wilson's Theorem?
...that the line separating the numerator and denominator of a fraction is called a solidus if written as a diagonal line or a vinculum if written as a horizontal line?
...that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type the complete works of William Shakespeare?
... that there are 115,200 solutions to the ménage problem of permuting six female-male couples at a twelve-person table so that men and women alternate and are seated away from their partners?

More did you know facts

Showing 7 items out of 75

Featured pictures

Image 1Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 4Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 11Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 18Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 18Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals